First Order Rate Constant Units

xiv.5: First-Order Reactions

1. Last updated

2. Save as PDF

Page ID

24267

In a first-order reaction, the reaction rate is straight proportional to the concentration of one of the reactants. Commencement-order reactions often have the general course A → products. The differential rate for a starting time-order reaction is as follows:

\[\textrm{charge per unit}=-\dfrac{\Delta[\textrm A]}{\Delta t}=g[\textrm A] \label{fourteen.4.5}\]

If the concentration of A is doubled, the reaction rate doubles; if the concentration of A is increased past a factor of ten, the reaction rate increases by a factor of x, so forth. Because the units of the reaction charge per unit are ever moles per liter per second, the units of a first-order rate constant are reciprocal seconds (s⁻¹).

The integrated charge per unit law for a outset-order reaction can be written in two different means: one using exponents and 1 using logarithms. The exponential form is equally follows:

\[[A] = [A]_0e^{−kt} \characterization{14.4.6}\]

where [A]₀ is the initial concentration of reactant A at t = 0; m is the charge per unit constant; and e is the base of the natural logarithms, which has the value 2.718 to 3 decimal places. Retrieve that an integrated rate law gives the human relationship betwixt reactant concentration and time. Equation \(\ref{xiv.4.six}\) predicts that the concentration of A will decrease in a smooth exponential curve over time. By taking the natural logarithm of each side of Equation \(\ref{xiv.four.6}\) and rearranging, nosotros obtain an culling logarithmic expression of the relationship between the concentration of A and t:

\[\ln[A] = \ln[A]_0 − kt \label{fourteen.4.7}\]

Because Equation \(\ref{14.four.7}\) has the form of the algebraic equation for a straight line, y = mx + b, with y = \ln[A] and b = \ln[A]₀, a plot of \ln[A] versus t for a first-order reaction should give a straight line with a slope of −one thousand and an intercept of \ln[A]₀. Either the differential rate law (Equation \(\ref{14.4.5}\)) or the integrated charge per unit police force (Equation \(\ref{14.4.7}\)) tin be used to determine whether a particular reaction is beginning social club.

Figure \(\PageIndex{1}\): Graphs of a first-order reaction. The expected shapes of the curves for plots of reactant concentration versus time (top) and the natural logarithm of reactant concentration versus fourth dimension (bottom) for a showtime-order reaction.

Start-order reactions are very mutual. We have already encountered two examples of offset-order reactions: the hydrolysis of aspirin and the reaction of t-butyl bromide with water to give t-butanol. Another reaction that exhibits apparent beginning-order kinetics is the hydrolysis of the anticancer drug cisplatin.

Cisplatin, the first "inorganic" anticancer drug to be discovered, is unique in its ability to cause complete remission of the relatively rare, but deadly cancers of the reproductive organs in young adults. The structures of cisplatin and its hydrolysis product are as follows:

Figure \(\PageIndex{two}\)

Both platinum compounds have four groups arranged in a square plane around a Pt(II) ion. The reaction shown in Figure \(\PageIndex{i}\) is important because cisplatin, the form in which the drug is administered, is not the form in which the drug is agile. Instead, at to the lowest degree one chloride ion must be replaced past water to produce a species that reacts with deoxyribonucleic acrid (DNA) to prevent cell partition and tumor growth. Consequently, the kinetics of the reaction in Figure \(\PageIndex{1}\) have been studied extensively to find ways of maximizing the concentration of the active species.

Note

If a plot of reactant concentration versus fourth dimension is not linear just a plot of the natural logarithm of reactant concentration versus time is linear, then the reaction is first order.

The rate law and reaction order of the hydrolysis of cisplatin are determined from experimental data, such as those displayed in Table \(\PageIndex{ane}\). The table lists initial rate information for four experiments in which the reaction was run at pH 7.0 and 25°C but with different initial concentrations of cisplatin. Because the reaction rate increases with increasing cisplatin concentration, we know this cannot be a zeroth-guild reaction. Comparison Experiments i and 2 in Table \(\PageIndex{1}\) shows that the reaction charge per unit doubles [(1.viii × x^−v M/min) ÷ (9.0 × ten⁻⁶ Thousand/min) = two.0] when the concentration of cisplatin is doubled (from 0.0060 Thousand to 0.012 M). Similarly, comparison Experiments 1 and iv shows that the reaction rate increases by a cistron of 5 [(4.5 × 10^−v M/min) ÷ (ix.0 × ten⁻⁶ One thousand/min) = 5.0] when the concentration of cisplatin is increased past a cistron of 5 (from 0.0060 M to 0.030 M). Considering the reaction rate is direct proportional to the concentration of the reactant, the exponent of the cisplatin concentration in the rate law must be 1, so the rate law is rate = g[cisplatin]¹. Thus the reaction is first order. Knowing this, we can calculate the rate abiding using the differential rate law for a beginning-order reaction and the information in whatsoever row of Tabular array \(\PageIndex{1}\). For example, substituting the values for Experiment three into Equation \(\ref{xiv.4.v}\),

iii.6 × 10^−v Thousand/min = k(0.024 Grand)

1.five × 10⁻³ min⁻¹ = k

Table \(\PageIndex{1}\): Rates of Hydrolysis of Cisplatin equally a Office of Concentration at pH 7.0 and 25°C

Experiment	[Cisplatin]0 (Thou)	Initial Rate (Yard/min)
1	0.0060	9.0 × x−half-dozen
ii	0.012	one.viii × 10−5
3	0.024	3.6 × 10−5
4	0.030	4.five × 10−5

Knowing the charge per unit constant for the hydrolysis of cisplatin and the rate constants for subsequent reactions that produce species that are highly toxic enables hospital pharmacists to provide patients with solutions that comprise merely the desired form of the drug.

Example \(\PageIndex{i}\)

At high temperatures, ethyl chloride produces HCl and ethylene by the following reaction:

\[\mathrm{CH_3CH_2Cl(one thousand)}\xrightarrow{\Delta}\mathrm{HCl(1000)}+\mathrm{C_2H_4(g)} \nonumber\]

Using the rate data for the reaction at 650°C presented in the following table, calculate the reaction order with respect to the concentration of ethyl chloride and decide the rate constant for the reaction.

Experiment	[CHiiiCH2Cl]0 (One thousand)	Initial Rate (G/s)
1	0.010	i.half dozen × 10−8
2	0.015	2.4 × 10−8
3	0.030	iv.eight × ten−8
4	0.040	6.4 × 10−8

Given: balanced chemical equation, initial concentrations of reactant, and initial rates of reaction

Asked for: reaction order and rate constant

Strategy:

1. Compare the data from two experiments to determine the issue on the reaction charge per unit of irresolute the concentration of a species.
2. Compare the observed effect with behaviors characteristic of zeroth- and first-guild reactions to determine the reaction order. Write the charge per unit police force for the reaction.

C Use measured concentrations and rate data from whatever of the experiments to discover the charge per unit constant.

Solution

The reaction order with respect to ethyl chloride is determined by examining the result of changes in the ethyl chloride concentration on the reaction rate.

A Comparing Experiments 2 and 3 shows that doubling the concentration doubles the reaction rate, so the reaction rate is proportional to [CH_iiiCH_iiCl]. Similarly, comparing Experiments 1 and 4 shows that quadrupling the concentration quadruples the reaction rate, over again indicating that the reaction rate is directly proportional to [CH_threeCH₂Cl].

B This behavior is feature of a first-society reaction, for which the charge per unit law is charge per unit = k[CH₃CH₂Cl].

C We tin calculate the rate constant (k) using any row in the table. Selecting Experiment i gives the post-obit:

1.60 × 10⁻⁸ M/s = k(0.010 K)

ane.6 × ten⁻⁶ due south^−one = k

Exercise \(\PageIndex{1}\)

Sulfuryl chloride (SO₂Cl₂) decomposes to And so₂ and Cl₂ by the following reaction:

So₂Cl_two(chiliad) → SO₂(g) + Cl₂(g)

Data for the reaction at 320°C are listed in the following tabular array. Summate the reaction order with regard to sulfuryl chloride and make up one's mind the rate constant for the reaction.

Experiment	[SO2Cl2]0 (M)	Initial Charge per unit (M/s)
1	0.0050	ane.x × 10−seven
2	0.0075	1.65 × 10−seven
3	0.0100	ii.20 × 10−7
4	0.0125	ii.75 × x−vii

Respond get-go order; k = two.2 × 10⁻⁵ s⁻¹

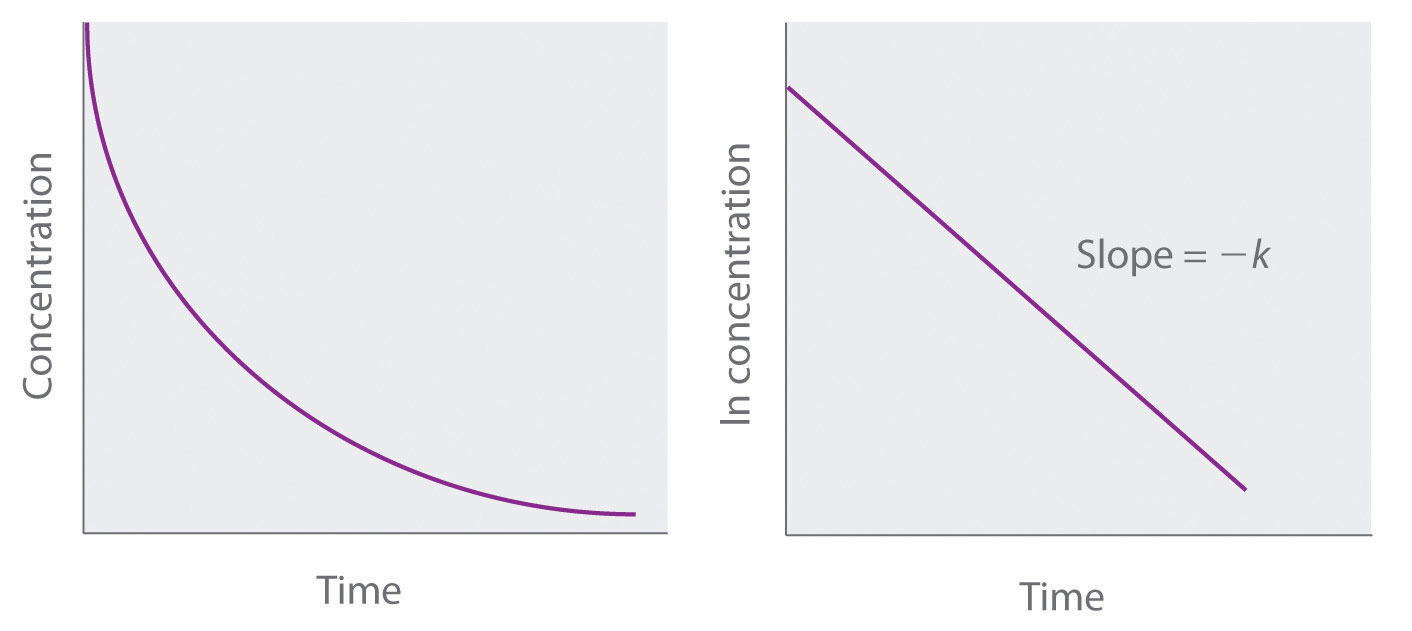
We can as well use the integrated rate law to determine the reaction rate for the hydrolysis of cisplatin. To practise this, nosotros examine the change in the concentration of the reactant or the product as a function of time at a single initial cisplatin concentration. Part (a) in Figure \(\PageIndex{iii}\) shows plots for a solution that originally contained 0.0100 G cisplatin and was maintained at pH seven and 25°C.

Figure \(\PageIndex{three}\): The Hydrolysis of Cisplatin, a Starting time-Order Reaction​. These plots testify hydrolysis of cisplatin at pH 7.0 and 25°C as (a) the experimentally determined concentrations of cisplatin and chloride ions versus fourth dimension and (b) the natural logarithm of the cisplatin concentration versus time. The straight line in (b) is expected for a first-lodge reaction.

The concentration of cisplatin decreases smoothly with time, and the concentration of chloride ion increases in a similar way. When we plot the natural logarithm of the concentration of cisplatin versus time, we obtain the plot shown in part (b) in Effigy \(\PageIndex{iii}\). The direct line is consistent with the beliefs of a system that obeys a first-order rate law. We tin can utilize whatsoever two points on the line to calculate the slope of the line, which gives us the rate constant for the reaction. Thus taking the points from part (a) in Figure \(\PageIndex{three}\) for t = 100 min ([cisplatin] = 0.0086 Yard) and t = 1000 min ([cisplatin] = 0.0022 M),

\(\begin{align}\textrm{slope}&=\dfrac{\ln [\textrm{cisplatin}]_{one thousand}-\ln [\textrm{cisplatin}]_{100}}{\mathrm{k\;min-100\;min}}
\\-one thousand&=\dfrac{\ln 0.0022-\ln 0.0086}{\mathrm{thou\;min-100\;min}}=\dfrac{-6.12-(-4.76)}{\mathrm{900\;min}}=-one.51\times10^{-3}\;\mathrm{min^{-1}}
\\yard&=1.5\times10^{-3}\;\mathrm{min^{-ane}}\end{align}\)

The gradient is negative because we are calculating the charge per unit of disappearance of cisplatin. Also, the rate abiding has units of min⁻¹ because the times plotted on the horizontal axes in parts (a) and (b) in Figure \(\PageIndex{iii}\) are in minutes rather than seconds.

The reaction order and the magnitude of the rate abiding we obtain using the integrated rate constabulary are exactly the same every bit those we calculated earlier using the differential rate police. This must be truthful if the experiments were carried out under the same weather condition.

 The Commencement-Gild Integrated Rate Law Equation:  https://youtu.exist/_JskhfxBAMI

Example \(\PageIndex{two}\)

If a sample of ethyl chloride with an initial concentration of 0.0200 M is heated at 650°C, what is the concentration of ethyl chloride after 10 h? How many hours at 650°C must elapse for the concentration to decrease to 0.0050 M (1000 = 1.6 × x⁻⁶ s⁻¹) ?

Given: initial concentration, rate constant, and time interval

Asked for: concentration at specified time and time required to obtain particular concentration

Strategy:

1. Substitute values for the initial concentration ([A]₀) and the calculated rate constant for the reaction (k) into the integrated charge per unit police for a first-social club reaction. Summate the concentration ([A]) at the given fourth dimension t.
2. Given a concentration [A], solve the integrated rate police for fourth dimension t.

Solution

The exponential class of the integrated charge per unit law for a first-order reaction (Equation \(\ref{14.iv.6}\)) is [A] = [A]₀ eastward ^−kt .

A Having been given the initial concentration of ethyl chloride ([A]₀) and having the rate constant of k = ane.vi × x⁻⁶ s⁻¹, we can use the rate constabulary to summate the concentration of the reactant at a given time t. Substituting the known values into the integrated rate police,

\(\begin{align}[\mathrm{CH_3CH_2Cl}]_{\mathrm{ten\;h}}&=[\mathrm{CH_3CH_2Cl}]_0e^{-kt}
\\&=\textrm{0.0200 M}(east^{\big{-(1.six\times10^{-6}\textrm{ due south}^{-1})[(10\textrm{ h})(60\textrm{ min/h})(threescore\textrm{ s/min})]}})
\\&=0.0189\textrm{ M}\stop{align}\)

We could too accept used the logarithmic form of the integrated rate constabulary (Equation \(\ref{14.4.7}\)):

\(\brainstorm{align}\ln[\mathrm{CH_3CH_2Cl}]_{\textrm{ten h}}&=\ln [\mathrm{CH_3CH_2Cl}]_0-kt
\\ &=\ln 0.0200-(1.6\times10^{-six}\textrm{ due south}^{-one})[(\textrm{10 h})(\textrm{lx min/h})(\textrm{60 s/min})]
\\ &=-3.912-0.0576=-three.970
\\ [\mathrm{CH_3CH_2Cl}]_{\textrm{10 h}}&=due east^{-3.970}\textrm{ M}
\\ &=0.0189\textrm{ M}\end{align}\)

B To summate the corporeality of time required to reach a given concentration, nosotros must solve the integrated charge per unit law for t. Equation \(\ref{14.4.vii}\) gives the following:

\(\brainstorm{marshal}\ln[\mathrm{CH_3CH_2Cl}]_t &=\ln[\mathrm{CH_3CH_2Cl}]_0-kt
\\kt &=\ln[\mathrm{CH_3CH_2Cl}]_0-\ln[\mathrm{CH_3CH_2Cl}]_t=\ln\dfrac{[\mathrm{CH_3CH_2Cl}]_0}{[\mathrm{CH_3CH_2Cl}]_t}
\\ t &=\dfrac{1}{thousand}\left (\ln\dfrac{[\mathrm{CH_3CH_2Cl}]_0}{[\mathrm{CH_3CH_2Cl}]_t} \right )=\dfrac{1}{1.6\times10^{-6}\textrm{ s}^{-1}}\left(\ln \dfrac{0.0200\textrm{ M}}{0.0050\textrm{ M}}\right)
\\ &=\dfrac{\ln 4.0}{one.6\times10^{-6}\textrm{ due south}^{-one}}=8.7\times10^5\textrm{ due south}=240\textrm{ h}=ii.4\times10^2\textrm{ h}\finish{align}\)

Exercise \(\PageIndex{2}\)

In the exercise above, y'all found that the decomposition of sulfuryl chloride (SO₂Cl₂) is first order, and you calculated the rate constant at 320°C. Use the form(due south) of the integrated rate law to find the amount of SO_twoCl₂ that remains after twenty h if a sample with an original concentration of 0.123 Grand is heated at 320°C. How long would information technology take for ninety% of the SO₂Cl₂ to decompose?

Answer 0.0252 Thousand; 29 h

Case Using the First-Society Integrated Rate Law Equation:

https://youtu.be/fLY6MtNl9-g

First Order Rate Constant Units,

Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_General_Chemistry_%28Petrucci_et_al.%29/14:_Chemical_Kinetics/14.05:_First-Order_Reactions

Posted by: stewartafre1969.blogspot.com

Share this post